Ley de Laplace
En física, la ecuación de Young-Laplace (/ləˈplɑːs/) es una ecuación diferencial parcial no lineal que describe la diferencia de presión capilar a través de la interfaz entre dos fluidos estáticos, como el agua y el aire. Esta diferencia se debe al fenómeno de la tensión superficial o tensión de pared. La tensión de pared sólo puede utilizarse para paredes muy finas. La ecuación de Young-Laplace relaciona la diferencia de presión con la forma de la superficie o pared. Es muy importante en el estudio de las superficies capilares estáticas.
En fisiología se conoce como ley de Laplace. Se utiliza para describir la presión dentro de los órganos huecos.
La ecuación lleva el nombre de Thomas Young, que desarrolló la teoría cualitativa de la tensión superficial en 1805, y de Pierre-Simon Laplace, que completó la descripción matemática al año siguiente. A veces también se denomina ecuación de Young-Laplace-Gauss: Carl Friedrich Gauss unificó los trabajos de Young y Laplace en 1830. Gauss derivó tanto la ecuación diferencial como las condiciones de contorno utilizando los principios del trabajo virtual de Johann Bernoulli.
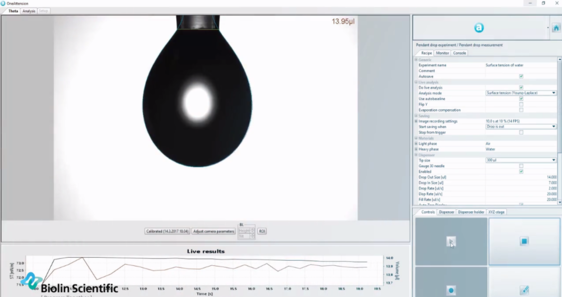
Los tensiómetros ópticos utilizan la ecuación de Young-Laplace para determinar automáticamente la tensión superficial de los líquidos en función de la forma de las gotas colgantes.
Preguntas y respuestas
P: ¿Qué es la ecuación de Young-Laplace?
R: La ecuación de Young-Laplace es una ecuación diferencial parcial no lineal que describe la diferencia de presión capilar a través de la interfase entre dos fluidos estáticos, como el agua y el aire.
P: ¿Con qué se relaciona?
R: Relaciona la diferencia de presión con la forma de la superficie o pared.
P: ¿Quién desarrolló esta teoría?
R: La teoría fue desarrollada por Thomas Young en 1805 y Pierre-Simon Laplace completó su descripción matemática al año siguiente. Posteriormente fue unificada por Carl Friedrich Gauss en 1830.
P: ¿Cómo se utiliza en fisiología?
R: En fisiología, se conoce como ley de Laplace y se utiliza para describir la presión en el interior de los órganos huecos.
P: ¿Qué fenómeno explica?
R: La ecuación de Young-Laplace explica el fenómeno de la tensión superficial o tensión de pared.
P: ¿La tensión de pared es aplicable a paredes gruesas? R: No, la tensión de pared sólo se puede utilizar para paredes muy finas.
