Nomograma: definición, uso y cómo leer un gráfico de cálculo
Descubre qué es un nomograma, su historia, uso práctico y cómo leer un gráfico de cálculo paso a paso. Guía clara para ingenieros y estudiantes.
Un nomograma o gráfico de alineación o abaque, es un gráfico de cálculo. Es un diagrama bidimensional que ofrece un cálculo de una función matemática.
La nomografía fue inventada en 1884 por el ingeniero francés Philbert Maurice d'Ocagne (1862-1938). Se utilizó durante muchos años para proporcionar a los ingenieros cálculos gráficos rápidos de fórmulas complicadas. Los nomogramas utilizan un sistema de coordenadas paralelas inventado por d'Ocagne en lugar de las coordenadas cartesianas estándar.
Un nomograma consiste en un conjunto de n escalas, una por cada variable de una ecuación. Conociendo los valores de n−1 variables, se puede encontrar el valor de la variable desconocida, o fijando los valores de algunas variables, se puede estudiar la relación entre las no fijadas.
El resultado se obtiene colocando una regla a través de los valores conocidos en las escalas y leyendo el valor desconocido desde el punto en que cruza la escala para esa variable. La línea virtual o dibujada creada por la regla se llama línea índice o isopleta.
Cómo leer un nomograma: pasos prácticos
- Identifica las escalas: localiza en el gráfico las etiquetas que corresponden a cada variable.
- Marca los valores conocidos: sitúa un punto o posiciona la regla sobre el valor de cada variable que conoces.
- Traza la línea índice: si el nomograma es de tipo alineación (escala recta), coloca una regla entre los puntos de las escalas conocidas; la intersección de la regla con la escala de la variable desconocida da el resultado.
- Interpolación: si la intersección cae entre marcas, interpola proporcionalmente para estimar el valor con mayor precisión.
- Verificación: cuando sea posible, comprueba el resultado con el cálculo algebraico o con otro método para asegurar exactitud.
Ejemplo sencillo
Para un nomograma que resuelve la multiplicación A × B = C mediante escalas logarítmicas paralelas (una escala por A, B y C):
- Localiza A = 2 en la escala A y B = 3 en la escala B.
- Coloca la regla uniendo 2 y 3; en la escala C la regla cruzará aproximadamente en 6.
- Así obtienes C ≈ 6 sin hacer la multiplicación aritmética manual.
Tipos principales de nomogramas
- Lineales o de escalas paralelas: los más comunes; cada variable tiene una escala recta. Permiten trazar una línea recta (isopleta) entre valores.
- Curvilíneos: alguna(s) escala(s) son curvas; se usan cuando la relación entre variables no se lineariza con transformaciones simples.
- Nomogramas en T y de tres escalas: estructura típica para ecuaciones de tres variables; las dos primeras escalas a los lados y la tercera en el centro o perpendicular.
- Nomogramas tipo red o reticulados: para ecuaciones con más variables o para permitir mayor precisión y opciones de lectura.
- Diagramas especializados: como las cartas de Smith en ingeniería de radiofrecuencia, que son variaciones gráficas para problemas concretos.
Cómo se construyen (principios básicos)
La construcción de un nomograma parte de la expresión matemática de la relación entre variables. Habitualmente se aplican transformaciones (logaritmos, recíprocos, potencias) para obtener escalas que permitan que la solución se represente por una línea recta uniendo dos valores. Los pasos generales:
- Elegir la forma matemática conveniente (por ejemplo transformar una multiplicación a suma de logaritmos).
- Determinar el tipo de escala (lineal, logarítmica, recíproca) para cada variable.
- Diseñar y posicionar las escalas en el plano de modo que la relación algebraica se traduzca en alineación geométrica.
- Calibrar las marcas y comprobar con ejemplos conocidos.
Ventajas y limitaciones
- Ventajas: permiten cálculos rápidos sin necesidad de máquinas; facilitan la visualización de cómo varía una variable al cambiar las otras; útiles en campo o en contextos donde se requiere rapidez.
- Limitaciones: precisión limitada (dependiente de la escala y de la habilidad del lector); no es práctico para problemas de muy alta dimensionalidad o con relaciones extremadamente complejas; requieren diseño cuidadoso para evitar errores de interpretación.
Aplicaciones históricas y actuales
- Ingeniería civil, naval y mecánica: cálculos de esfuerzo, flujo, resistencia, etc.
- Medicina: puntuaciones clínicas y riesgo (algunos scores clínicos se presentan como nomogramas para estimar probabilidades).
- Física y química: conversiones, diagramas termodinámicos simplificados.
- Astronomía y navegación: antes del advenimiento de calculadoras electrónicas se usaban para correcciones y transformaciones.
- Hoy en día se siguen usando cuando se desea una representación visual y rápida; además existen herramientas informáticas que generan nomogramas interactivos.
Consejos para una lectura precisa
- Utiliza una regla delgada y transparente o una tira guía para reducir error parallax.
- Si el nomograma es pequeño, emplea una lupa para mejorar la interpolación entre marcas.
- Comprueba unidades y rangos: muchas veces las escalas usan unidades distintas o están expresadas en potencias (por ejemplo, kW, m/s, etc.).
- Cuando trabajes con valores fuera del rango de las escalas, no extiendas —diseña o usa otro nomograma adecuado.
Recursos modernos
Con la llegada de software y páginas web, es posible crear y usar nomogramas digitales que permiten mayor precisión e interacción (zoom, ajuste de rangos, cálculo automático). Sin embargo, el principio geométrico clásico sigue siendo el mismo y comprender cómo leerlos y construirlos aporta intuición y rapidez para resolver problemas prácticos.
En resumen, un nomograma es una herramienta gráfica potente para representar relaciones matemáticas y efectuar cálculos rápidos y visuales. Aunque muchas de sus funciones las han sustituido las calculadoras y los ordenadores, siguen siendo valiosos por su claridad, simplicidad y capacidad de mostrar relaciones entre variables de forma inmediata.
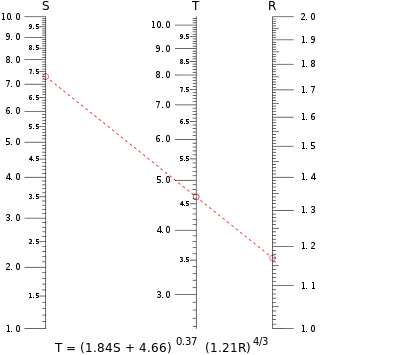
Un nomograma típico de escala paralela. Este ejemplo calcula el valor de T cuando S = 7,30 y R = 1,17 se sustituyen en la ecuación. La isopleta cruza la escala de T justo por debajo de 4,65.
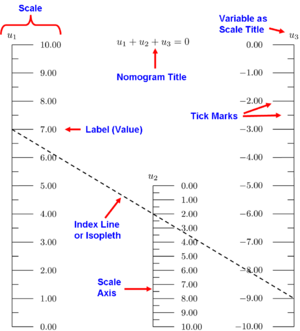
Componentes de un nomograma de escala paralela
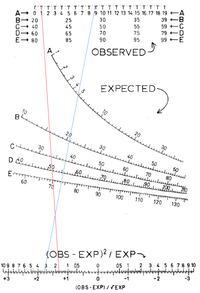
Nomograma de la distribución chi-cuadrado
Utilice
Los nomogramas se utilizaron ampliamente durante unos 75 años. Permitían realizar cálculos rápidos y precisos antes de la era de las calculadoras de bolsillo. Los resultados de un nomograma se obtienen de forma rápida y fiable dibujando una o varias líneas. El usuario no tiene que saber resolver ecuaciones algebraicas, buscar datos en tablas, utilizar una regla de cálculo o sustituir números en ecuaciones para obtener resultados. El usuario ni siquiera necesita conocer la ecuación subyacente que representa el nomograma.
Los nomogramas incorporan en su diseño el conocimiento del dominio. Por ejemplo, para crear nomogramas más grandes para una mayor precisión, el nomógrafo suele incluir sólo los rangos de escala que son razonables y de interés para el problema. Muchos nomogramas incluyen otras marcas útiles, como etiquetas de referencia y regiones coloreadas. Todos ellos proporcionan una guía útil para el usuario.
Al igual que la regla de cálculo, el nomograma es un dispositivo gráfico de cálculo analógico. Al igual que la regla de cálculo, su exactitud está limitada por la precisión con la que se pueden dibujar, reproducir, visualizar y alinear las marcas físicas. Los nomogramas pueden seguir utilizándose para comprobar una respuesta de otro cálculo más exacto, pero que puede dar lugar a errores.
Preguntas y respuestas
P: ¿Qué es un nomograma?
R: Un nomograma es un gráfico utilizado para el cálculo, que da un cómputo de una función matemática.
P: ¿Quién inventó el campo de la nomografía?
R: El campo de la nomografía fue inventado por Philbert Maurice d'Ocagne, un ingeniero francés, en 1884.
P: ¿Cuál era la finalidad de los nomogramas?
R: Los nomogramas se utilizaron durante muchos años para proporcionar a los ingenieros cálculos gráficos rápidos de fórmulas complicadas.
P: ¿De cuántas escalas consta un nomograma?
R: Un nomograma consta de un conjunto de n escalas, una para cada variable de una ecuación.
P: ¿Cómo se puede hallar el valor de una variable desconocida utilizando un nomograma?
R: Conociendo los valores de n-1 variables, se puede hallar el valor de la variable desconocida colocando una regla sobre los valores conocidos en las escalas y leyendo el valor desconocido a partir de donde cruza la escala para esa variable.
P: ¿Cómo se llama la línea virtual o trazada creada por la regla?
R: La línea virtual o trazada creada por la regla se denomina línea índice o isopleta.
P: ¿Qué tipo de sistema de coordenadas se utiliza en los nomogramas?
R: Los nomogramas utilizan un sistema de coordenadas paralelas inventado por d'Ocagne en lugar de las coordenadas cartesianas estándar.
Buscar dentro de la enciclopedia