Leyes de Newton
Isaac Newton (1642-1727) es ampliamente conocido como el padre de la dinámica, el estudio del movimiento. Desarrolló tres leyes que son la base de la mecánica clásica. Se cree que son ciertas porque los resultados de los experimentos realizados por los científicos coinciden con sus leyes.
Publicación original de las dos primeras leyes, en latín
Primera ley
- Si un cuerpo está en reposo, permanece en reposo o, si está en movimiento, se mueve con velocidad uniforme, hasta que se actúa sobre él con una fuerza neta.
Una "velocidad uniforme" significa que un objeto se mueve a una velocidad constante sin cambiar de dirección (es decir, en línea recta). Una "fuerza neta" significa que las fuerzas que actúan sobre el objeto no están equilibradas. En otras palabras, la primera ley establece dos cosas:
- Un objeto inmóvil sólo se moverá si hay una fuerza desequilibrada que actúe sobre él.
- Un objeto en movimiento sólo cambiará de velocidad o dirección si hay una fuerza desequilibrada que actúa sobre él.
La primera parte afirma que una mesa apoyada en el suelo no se moverá si no es empujada. Aunque la gravedad actúa sobre la mesa, tirando de ella hacia abajo, hay una fuerza de reacción del suelo que la empuja hacia atrás. Las fuerzas que actúan sobre la mesa están equilibradas, por lo que el objeto no se moverá.
La segunda parte es más difícil de entender. Una pelota que rueda por una superficie plana se ralentiza y acaba deteniéndose. Pero esto se debe a la fricción, que es una fuerza que frena la pelota. Una pelota que rueda por una pendiente también se ve afectada por la fricción, pero la fuerza de la gravedad que hace que se mueva es más fuerte. En un lugar sin las fuerzas de rozamiento, resistencia del aire y gravedad (por ejemplo, en el espacio exterior) un objeto en movimiento seguiría moviéndose en línea recta si no hubiera ninguna fuerza que lo frenara o cambiara su dirección.
Segunda ley
- Para una partícula de masa m, la fuerza neta F sobre la partícula es igual a la masa m por la aceleración a de la partícula:
F = m a {\displaystyle \mathbf {F} =m\mathbf {a} } 
.
La segunda ley de Newton establece que la aceleración de una partícula depende de las fuerzas que actúan sobre ella y de su masa. Para una partícula dada, si la fuerza neta aumenta, la aceleración aumenta. Para una fuerza neta dada, cuanta más masa tenga una partícula, menos aceleración tendrá.
Por ejemplo, el peso es una fuerza que sentimos en la Tierra, causada por la gravedad. El peso W de una partícula viene dado por
W = m g {\displaystyle \mathbf {W} =m\mathbf {g} } 
,
donde m es la masa de la partícula y g es la aceleración gravitatoria local (no confundir con G, la constante gravitatoria universal), aproximadamente igual a 9,8 metros por segundo2 (32 pies por segundo2 ) en la Tierra.
Podemos expresar la segunda ley de Newton en términos de momento. El momento p de una partícula se define como el producto de su masa m y su velocidad v:
p = m v {\diseño de la pantalla \mathbf {p} =m\mathbf {v} } 
.
La aceleración a de una partícula es la derivada temporal de su velocidad v:
a = d v d t {\mathbf {a} = {\frac {mathrm {d}} \mathbf {v} }{mathrm {d} t}}
.
Por lo tanto,
F = m a = m d v d t = d ( m v ) d t = d p d t {\displaystyle \mathbf {F} =m\mathbf {a} =m{\frac {\mathrm {d} }{\mathrm {d} t}}. \mathbf {v} }{mathrm {d} t}={frac {mathrm {d}(m\mathbf {v} )}{mathrm {d} t}={frac {mathrm {d} \...p... }{mathrm {d} t}}
.
Así, tenemos otra forma de enunciar la segunda ley de Newton:
- Para una partícula de masa m, la fuerza neta F sobre la partícula es igual a la derivada temporal del momento p de la partícula:
F = d p d t {{mathbf {F}} ={frac {mathrm {d}} \mathbf {p} } {\mathrm {d} t}} }{mathrm {d} t}}
.
En la mecánica clásica, las dos formas de la segunda ley, F = m a {\displaystyle \mathbf {F} =m\mathbf {a} } } y F = d p d t {\displaystyle \mathbf {F} = {\frac {\mathrm {d} \p... {{mathrm {d} t}}, son completamente equivalentes.} son completamente equivalentes. Nótese que suponemos que la masa m de una partícula no cambia.
Tercera ley
- Para cada acción, hay una reacción igual y opuesta. O toda acción reacciona siempre en sentido contrario.
Esto se entiende mejor con las bolas de billar, donde se pueden ver fácilmente los pares de acción/reacción de las fuerzas. Del mismo modo, cuando se patea un balón de fútbol, no sólo se mueve el balón, sino que se siente una fuerza en el pie.
El tamaño de las fuerzas en el primer objeto es igual al tamaño de la fuerza en el segundo objeto. La dirección de la fuerza sobre el primer objeto es opuesta a la dirección de la fuerza sobre el segundo objeto. Las fuerzas siempre vienen en pares: pares de fuerzas de acción y reacción iguales y opuestas.
En la naturaleza hay una gran variedad de pares de fuerzas de acción y reacción. Pensemos en la propulsión de un pez en el agua. Un pez utiliza sus aletas para empujar el agua hacia atrás. Pero un empuje sobre el agua sólo servirá para acelerar el agua. Como las fuerzas son el resultado de interacciones mutuas, el agua también debe empujar al pez hacia delante, impulsándolo a través del agua. El tamaño de la fuerza sobre el agua es igual al tamaño de la fuerza sobre el pez; la dirección de la fuerza sobre el agua (hacia atrás) es opuesta a la dirección de la fuerza sobre el pez (hacia adelante). Para cada acción, hay una fuerza de reacción igual (en tamaño) y opuesta (en dirección). Los pares de fuerzas de acción-reacción hacen posible que los peces naden.
Considera el movimiento de un coche de camino al colegio. Un coche tiene ruedas que giran hacia delante. Al girar hacia delante, las ruedas se agarran a la carretera y la empujan hacia atrás. Como las fuerzas son el resultado de interacciones mutuas, la carretera también debe empujar las ruedas hacia delante. El tamaño de la fuerza sobre la carretera es igual al tamaño de la fuerza sobre las ruedas (o el coche); la dirección de la fuerza sobre la carretera (hacia atrás) es opuesta a la dirección de la fuerza sobre las ruedas (hacia delante). Para cada acción, hay una reacción igual (en tamaño) y opuesta (en dirección). Los pares de fuerzas de acción-reacción hacen posible que los coches se desplacen por la calzada.
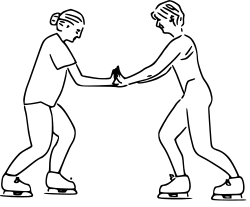
Tercera ley de Newton. Las fuerzas de los patinadores entre sí son de igual magnitud, y en direcciones opuestas
