Teorema de los esquemas de Holland: definición y su rol en algoritmos genéticos

Descubre el Teorema de los esquemas de Holland: definición, implicaciones y su rol en algoritmos genéticos para entender cómo los esquemas guían la evolución computacional.

Autor: Leandro Alegsa

15-01-2026 22:36

El teorema de los esquemas de Holland, también llamado teorema fundamental de los algoritmos genéticos, es una desigualdad que surge del análisis macroscópico de la dinámica poblacional en algoritmos genéticos. Establece que los esquemas cortos y de bajo orden cuya aptitud media es superior a la media poblacional tienden a aumentar su representación en generaciones sucesivas, con una tasa que depende de la selección y de los operadores de variación (cruce y mutación). El teorema fue propuesto por John Holland en la década de 1970 y, durante años, se consideró un pilar de la explicación de por qué los algoritmos genéticos pueden encontrar buenas soluciones. Posteriormente, investigaciones posteriores aclararon sus límites y mostraron que el Teorema del Esquema puede verse como un caso particular de la ecuación de Price cuando se utiliza la función indicadora del esquema como medida macroscópica; además, diversas publicaciones han criticado la interpretación simplificada del teorema y su uso como justificación única del llamado "hipótesis de los bloques de construcción".

Definición formal (versión clásica)

Sea H un esquema sobre cadenas binarias de longitud l. Denotando por m(H,t) el número de individuos que pertenecen a H en la generación t, por f(H) la aptitud media de esos individuos y por f̄ la aptitud media de la población, el teorema da una cota inferior para la esperanza del número de copias de H en la siguiente generación (t+1). En la formulación clásica, suponiendo selección proporcional, cruce de un punto con probabilidad pc y mutación bit a bit con probabilidad pm, se obtiene:

E[m(H,t+1)] ≥ m(H,t) · ( f(H) / f̄ ) · ( 1 − pc · δ(H)/(l−1) ) · (1 − pm)^{o(H)}

Donde:

o(H) es el orden del esquema: número de posiciones fijas (no comodines) en H.
δ(H) es la longitud definitoria: distancia entre la primera y la última posición fija en H (si hay una sola posición fija, δ(H)=0).
l es la longitud total de las cadenas.

En muchas exposiciones se aproxima (para pm pequeño) (1 − pm)^{o(H)} ≈ 1 − o(H)·pm, y la expresión resulta en una forma lineal aproximada que muestra la fracción de esquemas que sobreviven a la mutación y al cruce.

Qué significa en términos intuitivos

Si un esquema tiene aptitud media superior a la media poblacional (f(H) > f̄), la selección tiende a aumentar su número de copias: factor (f(H)/f̄) > 1.
Los esquemas cortos (δ pequeño) y de bajo orden (o pequeño) son menos propensos a ser destruidos por cruce y mutación, por lo que su retención es mayor. Por eso se habla de “bloques de construcción” (building blocks): partes pequeñas y buenas que la búsqueda recombina y amplifica.
La desigualdad es un límite inferior: no excluye que se formen nuevas copias de H por recombinación entre individuos que no pertenecían originalmente a H; ese efecto puede incrementar aún más la representación de H en la siguiente generación.

Supuestos y limitaciones

La formulación clásica asume selección proporcional; otras estrategias de selección (torneo, truncamiento, etc.) cambian la expresión y su interpretación.
Se suele asumir cruce de un punto y mutación independiente por bit. Con operadores más complejos (cruce uniforme, cruce múltiple, operadores dependientes de la estructura) la probabilidad de destrucción o creación de esquemas cambia.
El teorema es un resultado de corto plazo (predice el cambio esperado entre generaciones sucesivas) y de carácter agregativo: no describe la dinámica completa a largo plazo ni garantiza convergencia a óptimos globales.
La interpretación causal (que el teorema explica por sí solo la efectividad de los algoritmos genéticos) ha sido cuestionada: el teorema no cuantifica cuánto contribuyen realmente los esquemas a la búsqueda en escenarios reales con representaciones y problemas complejos.
Relación con la ecuación de Price: el teorema puede derivarse como caso particular de esta ecuación general de la selección cuando se toma la indicadora del esquema como rasgo, lo que muestra que el resultado es consistente con teorías más generales de la selección y no exclusivo de los AG.

Implicaciones prácticas

Favorece el uso de representaciones y operadores que preserven bloques cortos y de bajo orden cuando dichos bloques representan componentes útiles de la solución.
Parámetros: tasas de mutación muy altas y cruces que rompen frecuentemente las posiciones relevantes (gran δ) perjudican la preservación de buenos esquemas; en cambio, una mutación baja y cruces adecuados facilitan la recolección y combinación de bloques.
En problemas con dependencias entre genes (epistasis fuerte) los bloques útiles pueden ser largos o tener posiciones no contiguas; en esos casos la visión clásica del teorema pierde fuerza y conviene usar técnicas que aprendan dependencias (por ejemplo, algoritmos de estimación de distribución o operadores de cruce adaptativos).

Ejemplo sencillo

Consideremos cadenas binarias de longitud l = 6 y el esquema H = 1 * 1 * * *. Aquí o(H) = 2 (dos posiciones fijas: la 1 y la 3) y δ(H) = 3 − 1 = 2. Si en la generación t existen m(H,t) = 10 copias de H, la aptitud media f(H) = 1.2, la aptitud poblacional f̄ = 1.0, pc = 0.7 y pm = 0.01, la cota aproximada sería:

E[m(H,t+1)] ≥ 10 · (1.2 / 1.0) · (1 − 0.7 · 2/(6−1)) · (1 − 0.01)^{2}.

Evaluando numéricamente se obtiene una estimación de la esperanza de copias en la siguiente generación; la expresión muestra explícitamente cómo selección (ratio 1.2) y operadores (factores de conservación) actúan en sentido opuesto.

Conclusión

El teorema de los esquemas de Holland es una herramienta útil para entender, de forma cuantitativa y local, cómo la selección y los operadores genéticos afectan la abundancia esperada de patrones (esquemas) en una población. Sin embargo, no es una explicación completa de la eficacia de los algoritmos genéticos en todos los casos: sus supuestos, su carácter de cota inferior y su alcance a corto plazo deben tenerse en cuenta. En la práctica, su valor mayor es conceptual: orienta a diseñar representaciones y operadores que permitan preservar y combinar subestructuras prometedoras, mientras que para un análisis detallado de rendimiento conviene complementar con enfoques más fines (ecuación de Price, modelos de enlace, EDAs, experimentación empírica).

Un esquema, recordando la definición, es una plantilla que identifica un subconjunto de cadenas con similitudes en determinadas posiciones de la cadena. Los esquemas son un caso especial de los conjuntos de cilindros y, por tanto, forman un espacio topológico, lo que permite un tratamiento formal y matemático de estas colecciones de patrones.

Descripción

Considere cadenas binarias de longitud 6. El esquema 1*10*1 describe el conjunto de todas las cadenas de longitud 6 con 1 en las posiciones 1, 3 y 6 y un 0 en la posición 4. El * es un símbolo comodín, lo que significa que las posiciones 2 y 5 pueden tener un valor tanto de 1 como de 0. El orden de un esquema o ( H ) {\displaystyle o(H)} $o(H)$ se define como el número de posiciones fijas en el esquema, mientras que la longitud definitoria δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ es la distancia entre la primera y la última posición específica. El orden de 1*10*1 es 4 y su longitud definitoria es 5. La aptitud de un esquema es la aptitud media de todas las cadenas que coinciden con el esquema. La aptitud de una cadena es una medida del valor de la solución del problema codificado, calculada por una función de evaluación específica del problema. Utilizando los métodos establecidos y los operadores genéticos de los algoritmos genéticos, el teorema del esquema afirma que los esquemas cortos y de bajo orden con una aptitud superior a la media aumentan exponencialmente en las generaciones sucesivas. Expresado como una ecuación:

E ( m ( H , t + 1 ) ) ≥ m ( H , t ) f ( H ) a t [ 1 - p ] . {\displaystyle \operatorname {E} (m(H,t+1))\Ngeq {m(H,t)f(H) \Nsobre a_{t}[1-p]. } $\operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1-p].$

Aquí m ( H , t ) {\displaystyle m(H,t)} $m(H,t)$ es el número de cadenas que pertenecen al esquema H {\displaystyle H} $H$ en la generación t {\displaystyle t} $t$ f ( H ) {\displaystyle f(H)} $f(H)$ es la aptitud media observada del esquema H {\displaystyle H} $H$ y a t {\displaystyle a_{t}} $a_{t}$ es la aptitud media observada en la generación t {\displaystyle t} $t$ . La probabilidad de perturbación p {\displaystyle p} $p$ es la probabilidad de que el cruce o la mutación destruyan el esquema H {\displaystyle H} $H$ . Se puede expresar como

p = δ ( H ) l - 1 p c + o ( H ) p m {\displaystyle p={delta (H) \over l-1}p_{c}+o(H)p_{m}} $p={\delta (H) \over l-1}p_{c}+o(H)p_{m}$

donde o ( H ) {\displaystyle o(H)} $o(H)$ es el orden del esquema, l {\displaystyle l} $l$ es la longitud del código, p m {\displaystyle p_{m}} $p_{m}$ es la probabilidad de mutación y p c {\displaystyle p_{c}} $p_{c}$ es la probabilidad de cruce. Por lo tanto, un esquema con una longitud de definición más corta δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ tiene menos probabilidades de ser interrumpido.
Un punto que a menudo se malinterpreta es por qué el Teorema del Esquema es una desigualdad en lugar de una igualdad. La respuesta es, de hecho, sencilla: el Teorema desprecia la pequeña, aunque no nula, probabilidad de que una cadena perteneciente al esquema H {\displaystyle H} $H$ sea creada "desde cero" por la mutación de una sola cadena (o la recombinación de dos cadenas) que no pertenecía a H {\displaystyle H} $H$ en la generación anterior.

Limitación

El teorema de los esquemas se mantiene bajo el supuesto de un algoritmo genético que mantiene una población infinitamente grande, pero no siempre se traslada a la práctica (finita): debido al error de muestreo en la población inicial, los algoritmos genéticos pueden converger en esquemas que no tienen ninguna ventaja selectiva. Esto sucede en particular en la optimización multimodal, donde una función puede tener múltiples picos: la población puede derivar para preferir uno de los picos, ignorando los otros.

La razón por la que el Teorema del Esquema no puede explicar el poder de los algoritmos genéticos es que se mantiene para todas las instancias del problema, y no puede distinguir entre los problemas en los que los algoritmos genéticos funcionan mal, y los problemas para los que los algoritmos genéticos funcionan bien.

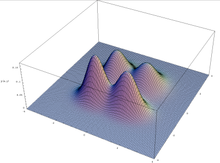
Gráfico de una función multimodal en dos variables.

Preguntas y respuestas

P: ¿Qué es el teorema del esquema de Holland?

R: El teorema del esquema de Holland es un teorema relativo a los algoritmos genéticos que dice que los individuos con una aptitud superior a la media tienen más probabilidades de prevalecer.

P: ¿Quién propuso el teorema del esquema de Holland y cuándo?

R: John Holland propuso el teorema del esquema de Holland en la década de 1970.

P: ¿Qué es un esquema en el contexto de los algoritmos genéticos?

R: En el contexto de los algoritmos genéticos, un esquema es una plantilla que identifica un subconjunto de cadenas con similitudes en determinadas posiciones de las cadenas.

P: ¿Cuál es la interpretación del teorema del esquema de Holland que se utilizó como base para las explicaciones del poder de los algoritmos genéticos?

R: La interpretación del teorema del esquema de Holland que se utilizó como fundamento de las explicaciones del poder de los algoritmos genéticos es que los individuos con una aptitud superior a la media tienen más probabilidades de prevalecer.

P: ¿Qué han demostrado las críticas al teorema del esquema de Holland?

R: Las críticas al teorema del esquema de Holland han demostrado que es un caso especial de la ecuación de Price con la función indicadora del esquema como medida macroscópica.

P: ¿Qué es un caso especial de los conjuntos cilíndricos?

R: Los esquemas son un caso especial de los conjuntos cilíndricos.

P: ¿Qué tipo de espacio forman los esquemas?

R: Los esquemas forman un espacio topológico.

Buscar dentro de la enciclopedia