Hexadecachorón (16-célula): definición del politopo regular convexo en 4D
Descubre el hexadecachorón: definición, propiedades y visualizaciones del 16-célula, el politopo regular convexo en 4D explicado de forma clara y visual.
En geometría cuatridimensional, una célula 16 es un policoro regular convexo o un politopo que existe en cuatro dimensiones. También se le conoce como hexadecachorón. Es uno de los seis polígonos regulares convexos descritos por primera vez por el matemático suizo Ludwig Schläfli a mediados del siglo XIX.
Conway lo denomina ortotopo para el complejo ortotopo, así como toda la clase de politopos cruzados.
Descripción y propiedades básicas
El hexadecachorón es el politopo regular convexo correspondiente al cross‑polytope en cuatro dimensiones (también llamado orthoplex). Sus propiedades más destacadas son:
- Símbolo de Schläfli: {3,3,4}.
- Vértices: 8.
- Aristas: 24.
- Caras (2‑caras): 32 (triángulos).
- Celdas (3‑caras): 16 (tetraedros regulares).
- Figura en el vértice: octaedro regular (por eso el último número 4 en {3,3,4}).
Coordenadas y modelo canónico
Una representación sencilla del hexadecachorón centrado en el origen de R^4 es tomar como vértices los vectores unitarios en las cuatro direcciones y sus opuestos:
(±1, 0, 0, 0), (0, ±1, 0, 0), (0, 0, ±1, 0), (0, 0, 0, ±1).
Con estas coordenadas, la longitud de cada arista es √2 y las 16 celdas son tetraedros regulares congruentes. Esta disposición evidencia que el hexadecachorón es el orthoplex en 4D, análogo al octaedro en 3D.
Dualidad y relaciones con otros politopos
El hexadecachorón es el dual del tesseracto (8‑célula o 8‑cell). Es decir, intercambia vértices por celdas y aristas por caras respecto al tesseracto. Forma parte de la familia de los cross‑polytopes (ortoplos) en dimensiones superiores: en n dimensiones el cross‑polytope tiene 2n vértices.
Simetría
Su grupo de simetría completo corresponde al grupo hiper-octaédrico en 4 dimensiones (tipo B4), con orden 384 si se incluyen reflexiones; el subgrupo de rotaciones (preservando la orientación) tiene la mitad de ese orden. Esta riqueza de simetría refleja la regularidad completa del politopo.
Visualización y proyecciones
Como todos los politopos de dimensión mayor a 3, el hexadecachorón se visualiza mediante proyecciones en 3D o mediante secciones. Las proyecciones canónicas muestran la estructura en 4 capas de vértices (según su coordenada), y las proyecciones estereográficas o ortogonales permiten apreciar la disposición de las 16 celdas tetraédricas alrededor del centro.
Aplicaciones y contextos
El estudio del hexadecachorón aparece en teoría de poliedros regulares, combinatoria geométrica, grupos de Coxeter y en visualización geométrica de dimensiones superiores. Su relación con el tesseracto y con las familias regulares de poliedros facilita comprender dualidad, simetría y generalizaciones en n dimensiones.
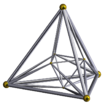
Un hexadecachorón
Geometría
El hexadecacoron es un miembro de la familia de los politopos llamados politopos cruzados, que existen en todas las dimensiones. Como tal, su policoro dual es el teseracto (el hipercubo de 4 dimensiones).
Está delimitado por 16 celdas, todas ellas tetraedros regulares. Tiene 32 caras triangulares, 24 aristas y 8 vértices. Las 24 aristas delimitan 6 cuadrados situados en los 6 planos de coordenadas.
Los ocho vértices del hexadecachorón son (±1, 0, 0, 0), (0, ±1, 0, 0), (0, 0, ±1, 0), (0, 0, 0, ±1). Todos los vértices están conectados por aristas, excepto los pares opuestos.
El símbolo de Schläfli del hexadecacorón es {3,3,4}. Su figura de vértice es un octaedro regular. Hay 8 tetraedros, 12 triángulos y 6 aristas que se encuentran en cada vértice. Su figura de arista es un cuadrado. Hay 4 tetraedros y 4 triángulos que se encuentran en cada arista.
Existe una forma de simetría inferior de la célula 16, llamada demitorio o 4-demicubo, miembro de la familia de los demihipercubos, y representada por h{4,3,3}, y puede dibujarse bicolor con células tetraédricas alternas.
Imágenes
· 
Proyección estereográfica
· 
Cuatro proyecciones ortográficas
· 
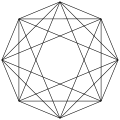
Una proyección ortogonal oblicua dentro de su polígono regular octogonal de Petrie, conectando todos los vértices excepto los opuestos.
· 
La célula 16 tiene dos construcciones de Wythoff, una forma regular y otra alternada, mostradas aquí como redes, la segunda representada por células tetraédricas de dos colores alternativamente.
· 
Una proyección 3D de una célula de 16 que realiza una doble rotación sobre dos planos ortogonales.
Teselaciones
Se puede teselar el espacio euclidiano de 4 dimensiones mediante 16 celdas regulares. Esto se llama el panal hexadecacórico y tiene el símbolo de Schläfli {3,3,4,3}. La teselación dual, el panal icositracórico, {3,4,3,3}, está formado por 24 celdas regulares. Junto con el panal teseráctico {4,3,3,4}, éstas son las únicas tres teselaciones regulares de R 4. Cada célula de 16 tiene 16 vecinos con los que comparte un octaedro, 24 vecinos con los que sólo comparte una arista y 72 vecinos con los que sólo comparte un punto. En esta teselación, veinticuatro celdas de 16 se encuentran en cualquier vértice.
Proyecciones
La proyección paralela de la celda 16 en el espacio 3 tiene una envoltura cúbica. Las celdas más cercanas y más lejanas se proyectan en tetraedros inscritos dentro del cubo, lo que corresponde a las dos formas posibles de inscribir un tetraedro regular en un cubo. Alrededor de cada uno de estos tetraedros hay otros 4 volúmenes tetraédricos (no regulares) que son las imágenes de las 4 celdas tetraédricas circundantes, llenando el espacio entre el tetraedro inscrito y el cubo. Las 6 celdas restantes se proyectan en las caras cuadradas del cubo. En esta proyección de la célula 16, todas sus aristas se encuentran en las caras de la envoltura cúbica.
La proyección en perspectiva de las 16 celdas en el espacio 3 tiene una envoltura tetraédrica de triakis. La disposición de las celdas dentro de esta envoltura es análoga a la de la proyección paralela de la primera celda.
La proyección paralela de vértice a vértice de la célula 16 en el espacio 3 tiene una envoltura octaédrica. Este octaedro puede dividirse en 8 volúmenes tetraédricos, cortando a lo largo de los planos de coordenadas. Cada uno de estos volúmenes es la imagen de un par de celdas de la 16-célula. El vértice de la 16 celda más cercano al espectador se proyecta sobre el centro del octaedro.
Por último, la proyección paralela del borde tiene una envoltura octaédrica acortada, y la proyección paralela de la cara tiene una envoltura bipiramidal hexagonal.
Páginas relacionadas
- 24 celdas
- Polychoron
Buscar dentro de la enciclopedia