Principio de Bernoulli
El principio de Bernoulli es una idea de la dinámica de los fluidos. Dice que a medida que la velocidad del fluido aumenta, la presión disminuye. La foto de la derecha muestra que esto ocurre. El aire de la parte ancha del tubo tiene una presión estática mayor que la de la parte fina. Para que el flujo sea constante, la cantidad de fluido que entra en el tubo debe ser igual a la que sale, por lo que la velocidad del fluido en la parte fina debe aumentar.
Cuando una fuerza actúa sobre un área, se denomina "presión". Una presión mayor empuja (acelera) el fluido hacia una presión menor. Por tanto, cualquier cambio en la velocidad de un fluido debe ir acompañado de un cambio en la presión (fuerza). Bernoulli vio que mientras el fluido se movía más rápidamente en la parte más pequeña del tubo, la presión se hacía menor. Hay que tener en cuenta que esto se refiere a los cambios de velocidad y presión a lo largo de un único trayecto del flujo y no se aplica a dos flujos diferentes con velocidades distintas.
La versión completa del principio de Bernoulli incluye tanto el trabajo por la presión como por los cambios en la energía potencial por los cambios de altura. En esta forma, el principio dice que el total de la presión, la energía cinética y la energía potencial es una constante. (Bernoulli no considera la viscosidad ni la compresibilidad).
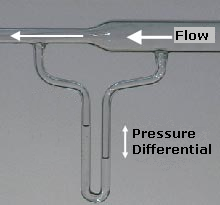
Un venturi que muestra el principio de Bernoulli. El agua de la derecha es más baja debido a la mayor presión en el tubo grande
Preguntas y respuestas
P: ¿Qué es el principio de Bernoulli?
R: El principio de Bernoulli es un concepto de la dinámica de fluidos que afirma que a medida que aumenta la velocidad de un fluido, disminuye la presión.
P: ¿Cómo se demuestra el principio de Bernoulli en la foto de la derecha?
R: La foto muestra que el aire de la parte ancha del tubo tiene una presión estática mayor que la de la parte fina, lo que hace que aumente la velocidad del fluido en la parte fina.
P: ¿Qué es la presión?
R: La presión es una fuerza que actúa sobre un área.
P: ¿Qué ocurre cuando cambia la velocidad de un fluido?
R: Un cambio en la velocidad de un fluido debe corresponderse con un cambio en la presión o en la fuerza.
P: ¿Se aplica el principio de Bernoulli a dos flujos distintos con velocidades diferentes?
R: No, el principio de Bernoulli sólo se aplica a los cambios de velocidad y presión a lo largo de una única trayectoria de flujo.
P: ¿Qué incluye la versión completa del principio de Bernoulli?
R: La versión completa del principio de Bernoulli incluye tanto el trabajo por la presión como por los cambios en la energía potencial por cambios en la altura.
P: ¿Qué no tiene en cuenta el principio de Bernoulli?
R: El principio de Bernoulli no considera la viscosidad ni la compresibilidad.
