Estereorradián (sr): definición y equivalencia en ángulos sólidos
Estereorradián (sr): definición, equivalencias y cómo mide ángulos sólidos en esferas. Explicación clara, ejemplos y aplicaciones para entender esta unidad del SI.
El estereorradián (símbolo: sr) o radián cuadrado es una unidad del SI. Es como un radián, pero para objetos 3D lisos, por ejemplo, una esfera. Un estereorradián equivale aproximadamente a una doceava parte de la superficie de una esfera, independientemente de su tamaño.
Definición y fórmula
El estereorradián mide ángulos sólidos. Para una superficie A sobre una esfera de radio r, el ángulo sólido Ω (en estereorradianes) viene dado por:
- Ω = A / r²
Esta relación muestra que el estereorradián es adimensional (relación de áreas), aunque en la práctica se usa el nombre y el símbolo sr para indicar que se trata de un ángulo sólido. El ángulo sólido total que abarca una esfera completa es
- Ω_esfera = 4π sr ≈ 12,5663706 sr
Por tanto, un estereorradián corresponde exactamente a la fracción 1/(4π) de la superficie total de una esfera, aproximadamente 0,079577 (≈ 7,96 %).
Expresiones útiles y ejemplos
- Elemento infinitesimal de ángulo sólido en coordenadas esféricas: dΩ = sin θ · dθ · dφ, con θ (colatitud) y φ (longitud).
- Ángulo sólido de un casquete esférico o de un cono de semángulo θ: Ω = 2π(1 − cos θ). Ejemplo: para θ = 30° (cos 30° = √3/2), Ω ≈ 0,84107 sr.
- Conversión a grados cuadrados: 1 sr = (180/π)² ≈ 3 282,80635 grados cuadrados. Inversamente, 1 grado cuadrado = (π/180)² sr ≈ 0,000304617 sr.
Usos y propiedades
- El estereorradián se usa en radiometría y fotometría para describir la distribución angular de energía o luz. Por ejemplo, la candela (unidad de intensidad luminosa) se define en relación con el flujo por unidad de ángulo sólido; y el lumen (flujo luminoso) se obtiene como candela × estereorradián (cd·sr = lm).
- Es una unidad derivada del SI y, aunque adimensional desde el punto de vista físico, su uso facilita la interpretación y el cálculo de cantidades angulares en 3D.
- El estereorradián es independiente del tamaño de la esfera usada para la medición: si una superficie subtensa un ángulo sólido Ω en una esfera de radio r, la misma superficie geométrica subtenderá el mismo Ω en cualquier otra esfera concéntrica (la relación A/r² permanece constante).
Resumen rápido
- Símbolo: sr (estereorradián).
- Definición: Ω = A / r² (área sobre r²).
- Ángulo sólido de la esfera completa: 4π sr ≈ 12,566 sr.
- Conversiones: 1 sr ≈ 3282,80635 deg², 1 deg² ≈ 0,000304617 sr.
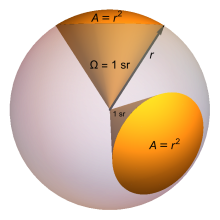
Un estereorradián en una esfera
Sphere vs Steradian
- La superficie de una esfera es 4 π r 2 {\displaystyle 4\pi r^{2}}
- La superficie de un estereorradio es simplemente r 2 {\displaystyle r^{2}}
Así, una esfera mide 4π estereorradianes, es decir, unos 12,57 estereorradianes. Asimismo, un estereorradián es 1/12,57, es decir, aproximadamente el 8% de una esfera. Y como medimos un ángulo, no importa el tamaño de la esfera, siempre medirá 4π estereorradianes.
Buscar dentro de la enciclopedia

