Ley de Snell: definición y fórmula de la refracción de la luz
Explica la Ley de Snell: definición, fórmula y ejemplos de refracción de la luz entre medios, índices de refracción y demostración vía el principio de Fermat.
La Ley de Refracción de Snell es la ley científica de la refracción de la luz u otras ondas. En óptica, la ley de Snell se refiere a la velocidad de la luz en diferentes medios. La ley establece que cuando la luz pasa a través de diferentes materiales (por ejemplo, del aire al vidrio) la relación de los senos del ángulo de incidencia (entrante) y el ángulo de refracción (saliente) no cambia:
sin θ 1 sin θ 2 = v 1 v 2 = n 2 n 1 {\displaystyle {\frac {\sin \theta _{1}}{\sin \theta _{2}}={\frac {v_{1}{v_{2}}={\frac {n_{2}}{n_{1}}}} 
Con cada θ {\displaystyle \theta }
como el ángulo medido desde la normal del límite, v {\displaystyle v}
como la velocidad de la luz en el medio respectivo (las unidades del SI son metros por segundo, o m/s). n {\displaystyle n} 
es el índice de refracción del medio.
El índice de refracción del vacío es 1 y la velocidad de la luz en el vacío es c {\displaystyle c}
. Cuando una onda pasa por el material donde el índice de refracción es n, la velocidad de la onda se convierte en c n {\displaystyle {\frac {c}{n}} 
.
La ley de Snell puede demostrarse mediante el principio de Fermat. El principio de Fermat establece que la luz se desplaza por el camino que requiere menos tiempo.
Interpretación y variables
De forma más práctica, la ley de Snell se expresa como:
- sin θ1 / sin θ2 = v1 / v2 = n2 / n1,
donde:
- θ1 es el ángulo de incidencia medido respecto a la normal de la superficie.
- θ2 es el ángulo de refracción en el segundo medio (también medido desde la normal).
- v1, v2 son las velocidades de la onda en los medios 1 y 2 respectivamente (en m/s).
- n1, n2 son los índices de refracción de los medios 1 y 2. Por definición n = c / v, siendo c la velocidad de la luz en el vacío.
Valores típicos: n del aire ≈ 1.0003, del agua ≈ 1.333 y del vidrio común ≈ 1.5. Cuando la luz entra en un medio con índice mayor, se aproxima a la normal; si entra en un medio con índice menor, se aleja de la normal.
Derivación breve a partir del principio de Fermat
El principio de Fermat plantea que la trayectoria seguida por la luz entre dos puntos es la que minimiza el tiempo de recorrido. Considerando dos medios con velocidades v1 y v2 separados por una interfaz plana y aplicando cálculo variacional (o derivando respecto al punto de cruce en la interfaz), se obtiene la condición que relaciona los ángulos en ambos lados de la interfaz, que es precisamente la ley de Snell. Esta demostración muestra que la ley de Snell no es arbitraria sino consecuencia de minimizar el tiempo de propagación.
Reflexión total interna y ángulo crítico
Si la luz viaja de un medio más refringente (n1) a otro menos refringente (n2), existe un ángulo crítico θc a partir del cual no hay refracción: toda la luz se refleja internamente. El ángulo crítico viene dado por:
- sin θc = n2 / n1 (válido cuando n1 > n2).
Para θ1 > θc se produce reflexión total interna, principio aprovechado en fibras ópticas y ciertas aplicaciones de guías de ondas.
Ejemplo numérico
Un ejemplo sencillo: luz que pasa del aire (n1 ≈ 1.0003, podemos aproximarlo por 1) al agua (n2 = 1.333) con incidencia θ1 = 30°:
- sin θ2 = (n1 / n2) sin θ1 ≈ (1 / 1.333) · 0.5 ≈ 0.375
- θ2 ≈ arcsin(0.375) ≈ 22.0°
Así, el rayo se acerca a la normal al entrar al agua.
Dependencia con la longitud de onda (dispersión)
El índice de refracción n depende generalmente de la longitud de onda de la radiación; este fenómeno se llama dispersión. Por ello, distintos colores (longitudes de onda) se refractan con ángulos ligeramente distintos al atravesar un prisma o una lente, produciendo separación de colores (por ejemplo, el arcoíris o la descomposición de la luz blanca en un prisma).
Aplicaciones prácticas
- Diseño de lentes y sistemas ópticos (cámaras, telescopios, microscopios).
- Prismas y espectroscopía (separación de colores por dispersión).
- Fibras ópticas, que emplean reflexión total interna para guiar la luz a largas distancias con pérdidas bajas.
- Mediciones de índices de refracción para caracterizar materiales.
Consejos y observaciones finales
- En la práctica experimental, se miden los ángulos respecto a la normal; asegúrese de referenciar correctamente los ángulos.
- Para ángulos pequeños (en radianes) se puede aproximar sin θ ≈ θ, con lo que la ley de Snell se aproxima a θ1 / θ2 ≈ n2 / n1.
- Recuerde que la ley es válida para ondas en general, no solo para luz: también se aplica a ondas sonoras, siempre que haya un cambio de velocidad entre medios y se pueda definir un frente de onda.
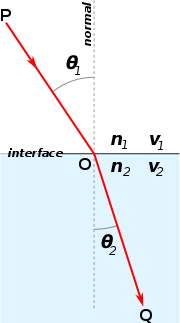
Refracción de la luz en la interfaz entre dos medios de diferentes índices de refracción, con n 2> n 1
Un rayo de luz incide en un prisma de cristal y se refracta
Historia
La idea tiene una larga historia. El problema llamó la atención de Héroe de Alejandría, Ptolomeo, Ibn Sahl y Huygens. Ibn Sahl descubrió realmente la ley de la refracción. En el Traité de la Lumiere, de 1678, Huygens mostró cómo la ley de los senos de Snell podía explicarse por la naturaleza ondulatoria de la luz, o derivarse de ella.
Preguntas y respuestas
P: ¿Qué es la Ley de Snell de la refracción?
R: La Ley de Refracción de Snell es la ley científica de la refracción de la luz u otras ondas. En óptica, establece que cuando la luz atraviesa materiales diferentes, la relación entre los senos de los ángulos de incidencia y refracción no cambia.
P: ¿Cómo se puede demostrar la Ley de Snell?
R: La Ley de Snell puede demostrarse mediante el Principio de Fermat, que establece que la luz viaja por una trayectoria que requiere el menor tiempo posible.
P: ¿Qué es el Principio de Fermat?
R: El Principio de Fermat establece que la luz viaja a lo largo de una trayectoria que tarda el menor tiempo posible.
P: ¿Qué son n y v en la Ley de Snell?
R: n es el índice de refracción de un medio y v es la velocidad de la luz en ese medio respectivo (medida en metros por segundo).
P: ¿Qué representa c en la Ley de Snell?
R: c representa la velocidad de la luz en el vacío, que tiene un índice de refracción igual a 1.
P: ¿Cómo se calcula la velocidad cuando una onda atraviesa un material con un índice de refracción n?
R: La velocidad se convierte en c/n cuando una onda atraviesa un material con un índice de refracción n.
Buscar dentro de la enciclopedia