Máquina abstracta
Un autómata (un autómata, varios autómatas) es un concepto de las matemáticas. A veces el concepto se llama máquina de estado. Es como una máquina abstracta.
A una máquina de este tipo se le puede dar entrada, que es rechazada o aceptada. Es como una máquina expendedora. Cuando se compra algo, hay que introducir monedas (o dinero) en la máquina. Si son las monedas correctas, se aceptan, y el artículo solicitado se deja caer para que pueda ser retirado. Si las monedas son incorrectas, se rechazan.
Internamente, el autómata tiene diferentes estados en los que puede estar. La introducción de datos puede cambiar (o no) su estado. Así, el autómata recorre toda la entrada, consumiendo un elemento (que los matemáticos llaman símbolo) cada vez. Cuando no queda ningún símbolo, el autómata se encuentra en un determinado estado. Puede tratarse de un estado final. En este caso, la entrada es aceptada. En caso contrario, la entrada es rechazada.
Si la máquina tiene un número contable y finito de estados, se llama máquina de estados finitos. Un diagrama que muestra todos los estados y transiciones de dicha máquina se denomina diagrama de estados finitos.
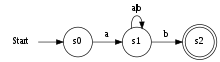
Representación habitual de un autómata en informática. Este autómata "acepta" todas las secuencias de las letras a y b que comienzan con una a y terminan con una b.
Problemas
Como en la vida real, hay máquinas que son demasiado complejas para entenderlas. Por ello, los matemáticos e informáticos se preguntan si un determinado autómata es mínimo. Si no es mínimo, debe haber otro autómata con menos estados que pueda hacer lo mismo. Un ejemplo de autómata es la máquina de Turing.
Preguntas y respuestas
P: ¿Qué es un autómata?
R: Un autómata es un concepto de las matemáticas que es como una máquina abstracta y a la que se le puede dar una entrada que es rechazada o aceptada.
P: ¿Cuál es otro término para un autómata?
R: A veces el concepto se denomina máquina de estados.
P: ¿Puede comparar un autómata con una máquina expendedora?
R: Sí, es como una máquina expendedora en la que hay que introducir monedas o dinero en la máquina y, si las monedas son las correctas, se deja caer el artículo solicitado para que pueda ser retirado.
P: ¿Qué ocurre cuando se da entrada a un autómata?
R: El autómata recorre toda la entrada, consumiendo un artículo cada vez, e internamente tiene diferentes estados en los que puede estar. Alimentarlo con entradas puede o no cambiar su estado.
P: ¿Qué ocurre cuando no quedan símbolos para el autómata?
R: Cuando no quedan símbolos, el autómata se encuentra en un estado determinado, que puede ser un estado final. En ese caso, se acepta la entrada; en caso contrario, se rechaza.
P: ¿Qué es una máquina de estados finitos?
R: Si la máquina tiene un número contable y finito de estados, se denomina máquina de estados finitos.
P: ¿Qué es un diagrama de estados finitos?
R: Un diagrama que muestra todos los estados y transiciones de una máquina de este tipo se denomina diagrama de estados finitos.
