Theorema egregium
El Teorema Egregio de Gauss (en latín, "Teorema notable") es un importante resultado de la geometría diferencial demostrado por Carl Friedrich Gauss. El teorema trata de la curvatura de las superficies. El teorema afirma que la curvatura puede determinarse únicamente midiendo los ángulos, las distancias y sus índices en una superficie. No es necesario hablar de la forma particular en que la superficie está incrustada en el espacio euclidiano tridimensional circundante. En otras palabras, la curvatura gaussiana de una superficie no cambia si se dobla la superficie sin estirarla.
Gauss presentó el teorema de esta manera (traducido del latín):
Por esta razón, la fórmula del artículo anterior conduce por sí misma al notable Teorema. Si una superficie curva se desarrolla sobre cualquier otra superficie, la medida de la curvatura en cada punto no cambia.
El teorema es "notable" porque la definición de partida de la curvatura gaussiana utiliza directamente la posición de la superficie en el espacio. Así que es bastante sorprendente que el resultado no dependa de su incrustación a pesar de todas las deformaciones de flexión y torsión sufridas.
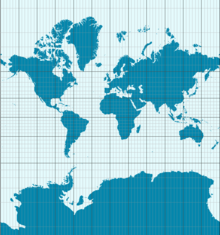
Una consecuencia del Theorema Egregium es que la Tierra no puede mostrarse en un mapa sin distorsión. La proyección Mercator, mostrada aquí, conserva los ángulos pero cambia la superficie. Por ejemplo, la Antártida se muestra mucho más grande de lo que realmente es.
